C/C++ 的变量在内存中的表示

阅读概要：

1. char
2. short, int 与 long
3. float 与 double
4. 数据类型转换时，内存中发生了什么

数据类型之间的区别，其本质在于对内存中的 $01$ 序列拥有不同的解释方式。为一个变量确定了数据类型，意味着对变量做了如下规定：

• 从变量的起始地址开始，有多大内存被征用
• 该段内存中的二进制序列，将以何种规则被解释

不同的数据类型与其所占有的内存大小

1 byte = 8 bits
1 bit 中文称为 1 位，是计算机表示数据的最小单位，可以表示 0 或 1 两个不同数值。

1. char

1 byte = 8 bits 如图所示，每个方块代表 1 位，8 个小方块的排列一共有 $2^8 = 256$ 种可能性，这也是 ASCII 码表大小为 256 的原因。

几个特殊符号的编码：

• '0' - 48
• 'A' - 65
• 'a' - 97

A - $65 = 2^6 + 2^0$，在内存中的样子如下图所示

2. short, int, long 等有符号数

以 short 为例， 2 bytes = 16 bits，$2^{16}$ 种可能。由于有符号，去掉 1 位，最大可以表示 $2^{15}-1$，最小可以到 $-2^{15}$。

要在内存中表示有符号数，必须要掌握三个概念：原码、反码和补码。

在介绍这三个概念的具体含义之前，我们先看一个 short 类型的 +7 在内存中怎么表示（最高位表示符号位，0为正，1为负）：

我们直接将 +7 的符号位置为 1，得到 -7 的表示：

但是如此一来， $(+7)+(-7)=-14$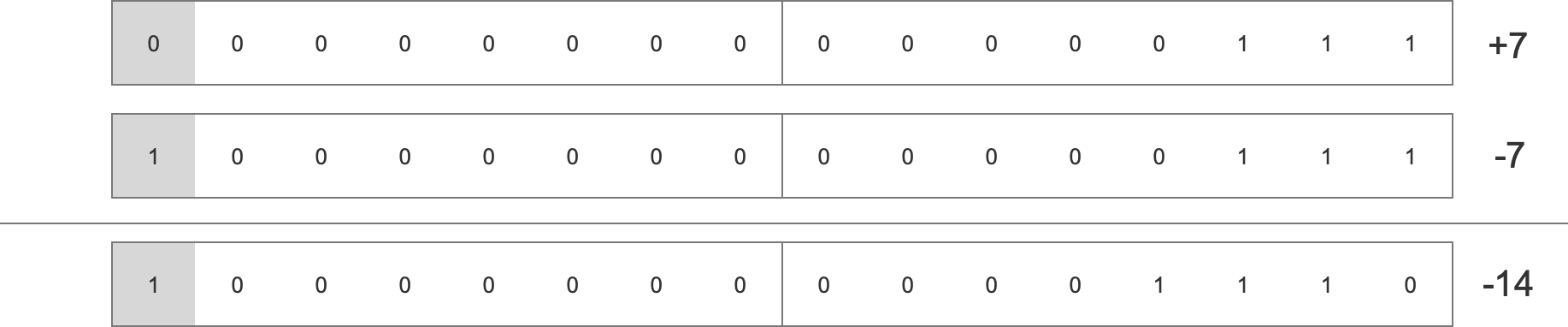

这显然是很不合理的。我们的目标是使得计算机在内存中操作 $(+7)+(-7)$ 时，得到的结果为 0。即如图所示，找到一个 $?$ 表示 $-7$，使得 $? + (+7) $ 得到所有位都为 0：

我们很难一下子找到一个 $?$ 使得其与 $+7$ 相加得到全零位。但是我们可以快速找到一个 $s$ 使得 $s + (+7)$ 的每一位均为 $1$ —— 将 $+7$ 按位取反来表示 $s$ 即可。

得到 $s$ 后，我们用 $s+ 1$ 表示 $?$，从而，$? + (+7) = 1+s+(+7)$ 的每一位均为 $0$。

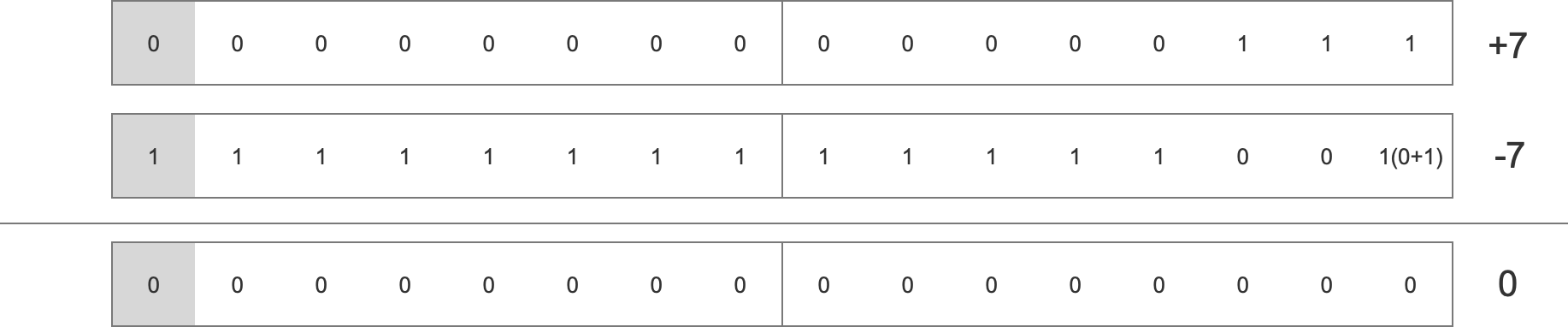
我们将 $s$ 称为反码，$?$ 为补码，原本的表示即为原码。计算机的内存中有符号数字的表示均采取“补码”。

总结一下，内存中所有有符号数以“补码”的形式表示，一个数的“补码”的规则为：

• 正数与 $0$ 的补码是自己。
• 负数的补码是其对应正数按位取反再加 1。

3. float 与 double

如上图所示，表示的数字为 $(-1)^{sign}\times 1.demical_part \times 2^{\ exponential_part-127}$。其中，$demical_part$ 的每一位的含义如下图所示：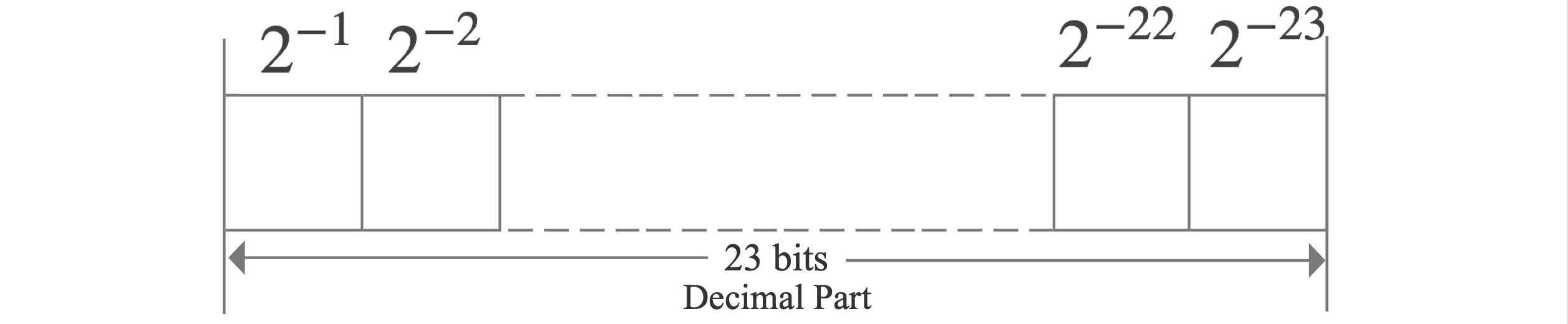

以浮点数 $7.0$ 的表示为例：
\begin{equation}
\begin{aligned}
7.0\ &= 3.5 \times 2^1\
&= 1.75 \times 2^2
\end{aligned}
\end{equation}

其中

因而，浮点数 $7.0$ 在内存中的表示如下图所示：

4. 数据类型转换时，内存中发生了什么

大端：高位在前，低位在后（符合人类阅读习惯）
小端：低位在前，高位在后（符合计算机处理习惯）

只有读取的时候，才必须区分字节序，其他情况都不用考虑

4.1 short 与 char

1
2
3

char ch = 'A';
short s = ch;
cout << s << endl; // 65

1
2
3

short s = 65;
char ch = s;
cout << ch << endl; // A

4.2 short 与 int

$s = 1033 = 2^{10} + 2^{3} + 2^{0}$

1
2
3

short s = 1033;
int i = s;
cout << i << endl; // 1033

$i = 8421378 = 2^{23} + 2^{15} + 2^{1}$

1
2
3

int i = 8421378;
short s = i;
cout << s << endl; // -32766

保留低 $16$ 位，得到 $s$ 的内存表示如图，short 中按照 “补码” 来对内存表示解码，而符号位为 $1$，因而对 $s$ 的每一位取反再加 $1$ 得到原码 $s’ = 32766$，因而 $s = -32766$

1
2
3

short s = -1;
int i = s;
cout << i << endl; // -1

用符号位补齐高位。

4.3 int 与 float

1
2
3

int i = 7;
float f = i;
cout << f << endl; // 7.0

这计算机会自动进行计算，float f 的内存长啥样，而不是直接复制 i 的内存到 f。

1
2
3

int i = 5;
float f = *(float*)&i;
cout << f << endl; // 7.00649e-45

这个就是将 i 的内存按照 float 的方式解释，因而得到一个很小的小数。
$decimal_part = 2^{-21} + 2^{-23}$
$exponential_part = 2^{-127}$

4.4 short 与 float

1
2
3

float f = 7.0;
short s = *(short*)&f;
cout << s << endl; // 小端机器为 0，大端机器为 16608 = pow(2,14) + pow(2,7) + pow(2,6) + pow(2,5)

• Next Post →